introduction
简单的常微分方程求解问题通式,我们的问题是从这个方程组入手,得到y关于x的函数关系,但是解析解一般难以求解,因此从数值解求法入手
\[
\begin{cases}
\frac{dy}{dx} = f(x, y) &x \in [a, b]\\
y(a) = y_0
\end{cases}
\] \(Lipschitz条件: |f(x, y_1) - f(x,
y_2)| \leq L|y_1 - y_0|, x \in [a, b]\)
当方程组中二元函数关系f满足该条件时,常微分方程有解
Lipschitz条件可以理解为:在任意x属于[a. b]的闭区间中,f(x. y)的任意一条纵向曲线都是导数有界
Euler方法
从三个角度理解欧拉方法的公式由来
差商近似导数 \[ \frac{f(x_{n+1}) - f(x_{n})}{x_{n+1} - x_n} = f(x_n, y_n) \\ \Rightarrow f(x_{n+1}) = f(x_n) + hf(x_n, y_n) \]
数值积分方法 \[ f(x_{n+1}) = f(x_n) + \int_{x_n}^{x_{n+1}}f(x, y)dx \\ 使用积分矩形近似 \Rightarrow f(x_{n+1}) = f(x_n) + hf(x_n, y_n) \]
Taylor展开方法 \[ f(x_{n+1}) = f(x_n) + hf(x_n, y_n) \\ 仅使用泰勒展开到一阶导数的程度来近似 \]
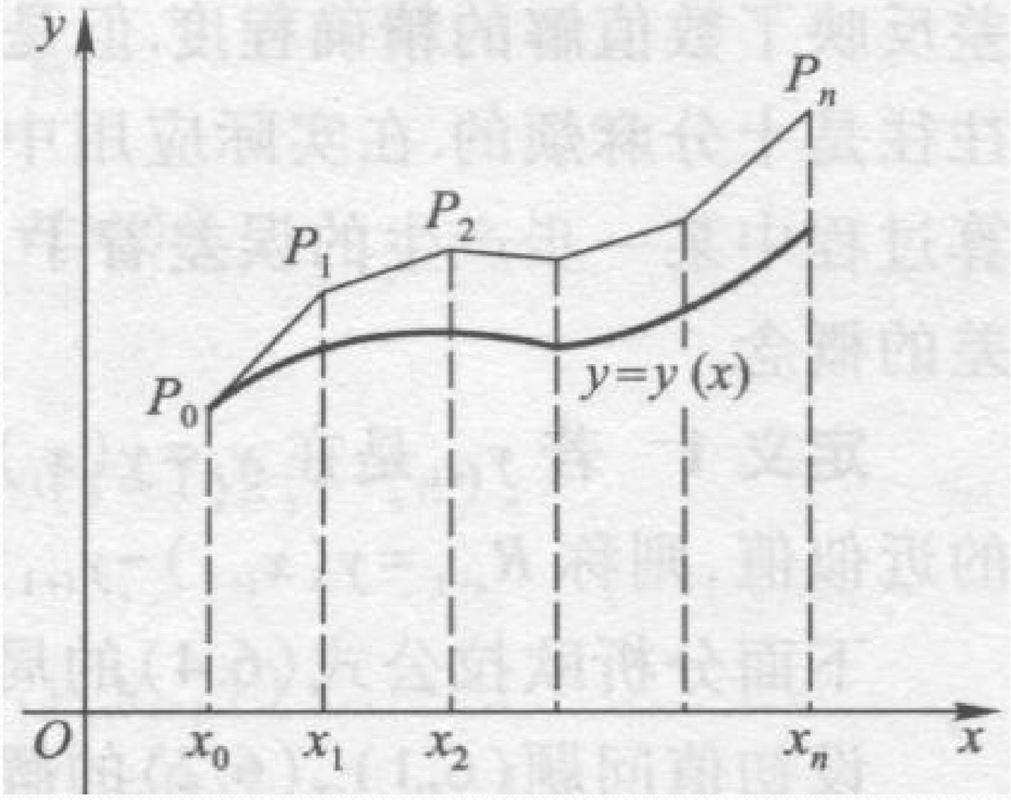
可以看出Euler方法会造成误差累积,拟合程度较差
改进Euler方法
改进Euler公式
改进Euler方法的特点在于使用两个端点的导数平均值作为延伸斜率,公式如下 \[ \begin{cases} \overline{y_{i + 1}} = y_i + h*f(x_i, y_i) \\ y_{i + 1} = y_i + \frac{h}{2} * [f(x_i, y_i) + f(x_{i + 1}, \overline{y_{i + 1}})] \end{cases} \] 公式中可以看出先使用Euler公式初步推算出 \(y_{i + 1}\)的值,再使用这个值在梯形公式中代出真正的\(y_{i + 1}\)
另外一种改进Euler方法的写法如下,该种公式呈现形式用于方便计算机编程 \[ \begin{cases} y_p = y_i + h*f(x_i, y_i) \\ y_q = y_i + h*f(x_{i + 1}, y_p) \\ y_{i + 1} = \frac{(y_p + y_q)}{2} \end{cases} \]
收敛阶的概念
整体截断误差:\(e_i = y(x_i) - y_i\),对于某一个数值计算方法,计算出每一个点上精确值和估算值的差值,称为整体截断误差,但这种方法一般都非常麻烦
局部阶段误差:\(R_{i+1} = y(i+1) - y_{i + 1}\),$y_{i + 1} \(的运算结果建立在\)y(x_i) = y_i\(的基础上,得到的\)R_{i+1}$误差值称为局部截断误差
收敛阶定义:如果一个数值方法的局部截断误差是\(O(h^{p + 1})\),那么该方法是p阶的
改进Euler方法的收敛阶分析:根据泰勒公式展开,得到收敛阶为2

Runge-Kutta方法
为了应对开始题目,先提出重要的经典四阶龙格库塔方法 \[ \begin{cases} y_{ i + 1 } = y_i + {h \over 6} * (K_1 + 2K_2 + 2K_3 + k_4)\\ K_1 = f(x_i, y_i)\\ K_2 = f(x_i + {h \over 2}, y_i + {h \over 2}K_1)\\ K_3 = f(x_i + {h \over 2}, y_i + {h \over 2}K_2)\\ K_4 = f(x_i + h, y_i + hK_4) \end{cases} \]