插值多项式
什么是插值问题?
已知一系列离散点,需要找到一个多项式,在这些结点上数值相等,其他结点上数值近似,所以插值公式存在以下两个问题
- 不是次数越高越好
- 存在误差,详见插值多项式的余项
对于目标插值多项式\(p_n(x) = a_0+a_1x+a_2x^2+...+a_nx^n\),列出一下方程 \[ \begin{cases} a_0+a_1x_0+a_2{x_0}^2+....+a_n{x_0}^n = f(x_0)\\ a_0+a_1x_1+a_2{x_1}^2+....+a_n{x_1}^n = f(x_1)\\ ......\\ a_0+a_1x_n+a_2{x_n}^2+....+a_n{x_n}^n = f(x_n) \end{cases} \] 显然\(x_0 \thicksim x_n\)和\(f(x_0) \thicksim f(x_n)\)都是已知量,所以提取系数矩阵,得到经典Vandacomde行列式 \[ \begin{vmatrix} 1 & x_0 & {x_0}^2 & ... & {x_0}^n\\ 1 & x_1 & {x_1}^2 & ... & {x_1}^n\\ ... & ...\\ 1 & x_n & {x_n}^2 & ... & {x_n}^n\\ \end{vmatrix} \] 由给定离散点可知,所有\(x_i\)都不相等,所以该Vandamonde行列式不为0,因此系数有唯一解
但是一般计算差值不等式的待定系数时不会硬解线性方程组,因此下面引入两种插值方法——lagrange插值公式和Newton插值公式
插值多项式余项推导
插值多项式余项定理:
若\(f(x)\)在区间\([a, b]\)上有直到\(n+1\)阶导数,\(p_n(x)\)为\(f(x)\)在n+1各结点下的n次插值多项式,则对\(\forall x \in [a, b]\)都有 \[ R_n(x) = f(x) - p_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}w_{n+1}(x) \\其中w_{n+1}(x) = \prod_{i = 0}^{n}(x - x_i) \]
余项公式证明如下:
已知原函数\(f(x)\),我们将用n次插值多项式\(p_n(x)\)去拟合
设\(R_n(x) = f(x) - p_n(x)\), 其中插值点\(x_0, x_1, ...x_n\)带入时\(p_n(x)\)完全等于\(f(x)\),因此我们可以确定\(R_n(x)\)一定有零点\(x_0, x_1, ...x_n\)
因此设 \[ f(x) = p_n(x) + k(x)w_{n+1}(x) \\即 R_n(x) = k(x)w_{n+1}(x) \]
此时我们要求的是待定系数\(k(x)\)
设辅助函数 \[ F(t) = f(t) - p_n(t) - k(x)w_{n+1}(t)\\ 其中 x为[a, b]中任意一个不等于x_i的存在,而t为[a, b]中任意值 \] 注意这一步中,我们采用变换主元法,将主元设置为
t,而x变为参量根据这一个辅助函数,我们可以得到以下两个推论
推论一: \[ F(x) = F(x_0) = F(x_1) = ... = F(x_n) = 0\\ 当主元t = x时,原函数f(x)和p_n(x) + k(x)w_{n+1}(x)完全相等,因此有t = x这个零点 \] 推论二:
对主元t进行求导,得 \[ F^{(n+1)}(t) = f^{(n+1)}(x) - k(x)(n+1)!\\ \] p_n(x)为n次多项式,因此在n+1阶求导后归零,\(w_{n+1}(x)\)为n+1阶多项式,首项系数为1,因此求导后得到阶乘
根据推论一,得到F(x)有n+2个零点,根据Rolle定理,得到F‘(x)有n+1个零点,以此类推,最终得到\(F^{(n+1)}(x)\)至少有一个零点
设该零点为\(x = \xi\),得到 \[ f^{(n+1)}(x) - k(x)(n+1)! = 0\\ \Rightarrow k(x) = \frac{f^{(n+1)}(x)}{(n+1)!}\\ 余项R_n(x) = k(x)w_{n+1}(x) = \frac{f^{(n+1)}(x)}{(n+1)!}w_{n+1}(x) \] 得证
Lagrange插值公式
Lagrange插值公式适用于一次性给定所有已知点的多项式待定系数计算,其公式如下 \[ 对于给定的离散点x_i(0 \le i \le n)和y_i(0 \le i \le n)\\ p_n(x) = \sum_{i = 0}^{n}y_i\prod_{j = 0 \atop j \ne i}^{n}\frac{x-x_j}{x_i-x_j} \] 注意Lagrange插值公式的基函数为 \[ l_k(x_i) = \begin{cases} 1, i = k\\ 0, i \ne k \end{cases} \] 这样的基函数对标上一条Lagrange插值公式中\(y_i\)右侧的连乘部分
Newton插值公式
Newton插值公式
Newton插值公式适用于节点数存在变化的离散点进行插值,公式如下 \[ p_n(x) = f(x_0) + \sum_{i=1}^{n}f[x_0,...x_i]\prod_{j=0 \atop j \ne i}^{i-1}(x-x_j) \] 注意Newton插值公式的基函数为\(\begin{cases}\psi_0(x)=1\\ \psi_i(x)= \prod_{j=0}^{i-1}(x-x_j) \end{cases}\)
此处列出差商公式 \[ f[x_0, x_1, ..., x_n] = \frac{f[x_1, x_2, ..., x_n] - f[x_0, x_1, ...,x_{n-1}]}{x_n - x_0} \] 以及其等价变式 \[ f[x_0, x_1, ..., x_n] = \frac{f[x_1, x_2, ..., x_{n - 2}, x_{n}] - f[x_0, x_1, ...,x_{n-1}]}{x_n - x_{n-1}}\\ 此处可以理解为分子右边中的x_{n-1}元素是x_0之前的一个元素,这样就能与上一条公式对齐 \]
Newton插值公式推导
由一阶插值公式可得 \[ f(x) = f(x_0) + f[x, x_0](x - x_0) \]
此时使用插值递推公式 \[ f[x, x_0, x_1, ..., x_n] = \frac{f[x, x_0, x_1, ..., x_{n-1}] - f[x_0, x_1, ..., x_n]}{x-x_n}\\ \Rightarrow f[x, x_0, x_1, ..., x_{n-1}] = f[x_0, x_1, ..., x_n] + (x - x_n)f[x, x_0, x_1, ..., x_n]\\ 此递推公式旨在当已知点从x_{n-1}扩展到x_n时,使用该式进行差商地推 \]
因此有如下Newton插值公式递推过程
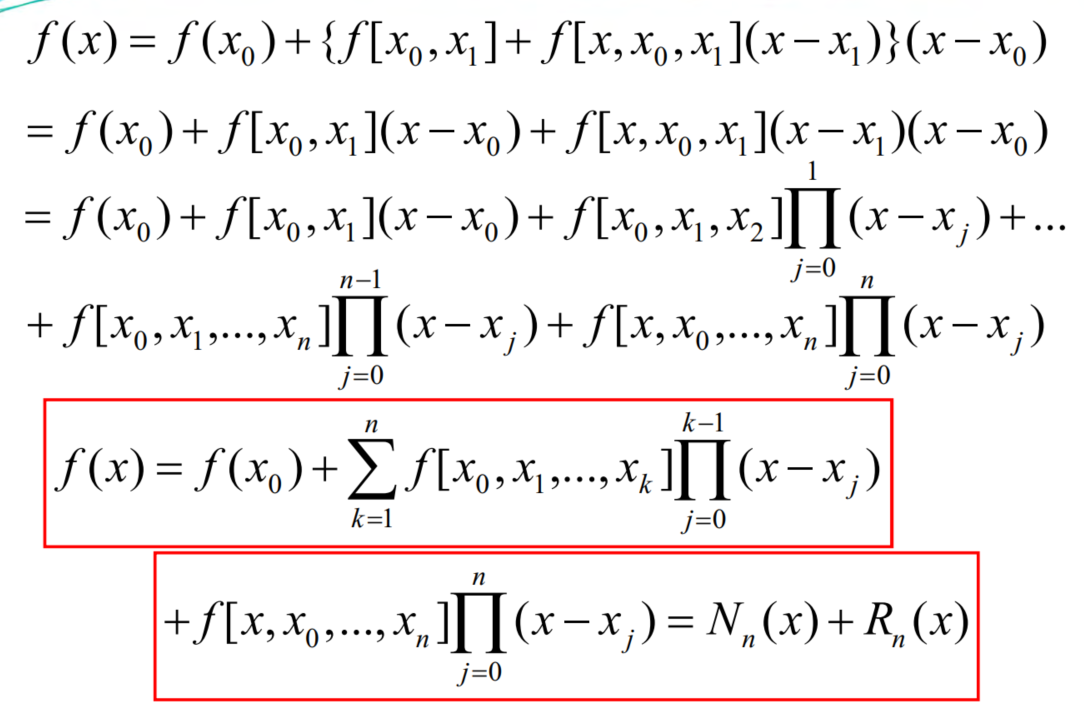
Newton插值公式余项
由上述Newton插值公式推导过程中显示的余项可以看出 \[ R_n(x) = f[x, x_0, x_1, ...., x_n]w_{n+1}(x) \] 对比插值多项式的统一余项公式 \[ R_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}w_{n+1}(x) \] 得到 \[ \frac{f^{(n+1)}(\xi)}{(n+1)!} = f[x, x_0, x_1, ...., x_n], \xi \in (a,b) \] 由此可以看出差商和导数的关系
分段低次插值
为了避免引用所有已知点而造成插值过拟合的现象,在某些问题中可以采用分段低次插值的方法,也就是只是用一系列已知点中的部分(只用两个点的线性插值、只用三个点的二次插值)来求插值多项式中某一个未知点的函数值
Hermite插值
引理:当有n+1个条件数时,则至高能构造出n阶插值多项式
这里条件数指的是已知函数点或者是已知导数点(任意阶导数)
解题步骤
- 确定多项式次数(条件数减一)
- 使用已知的函数点个数先构造Lagrange插值多项式(Newton也可,但计算量随已知点增多而增多),在后面添加形如\((x-x_i), (x_i为函数已知点)\)的连乘式,为了能够凑齐多项式整体的次数,需要在这个连乘式前乘形如\(A+Bx+Cx^2+...\)的多项式,这里的待定系数多项式次数具体由需要补齐的 次数而定(也可以说由当前已知的导数数量而定)
- 对待定系数的多项式进行求导,带入导数值,对所有待定系数进行求解
最小二乘法拟合
当我们不需要确切拟合每一个已知函数点的时候,仅需要拟合出“形状”,此时可以考虑最小二乘法拟合
最小二乘法拟合函数
设我们最终要求的函数为\(\psi(x)\),则\(\psi(x)\)要满足一下这个特点 \[ \sum_{i = 0}^{n} [\psi(x_i) - y_i]^2 为最小值 \] 我们要解决的问题就是找到这个\(\psi(x)\)来满足最小二乘判定的最小值
最小二乘法函数推导
设\(\psi(x) = F(a_0, a_1, a_2, ..., a_n, x), 这里F函数是以a_i为系数,x为主元的多项式函数\),则我们要求得函数满 足以下特性 \[ S(a_0, a_1, a_2, ..., a_m) = \sum_{i = 0}^{n}[F(a_0, a_1, a_2, ..., a_m, x_i) - y_i]^2 为最小值\\ \]
以上公式注意两点
这里使用已知点带入x_i,该式的本质已经从一个一元多项式函数变成了多元一次多项式
这里多项式F的次数仅使用到m,多项式次数m和已知点n(已知量n+1)是\(m \le n\)的关系。因为当次数提高到m,意味着多项式待定系数有m+1个,而已知量只有n+1组,因此从线性方程组可解性上来判断,待定系数的数量也受此限制
根据多元函数最小值判定的必要条件,得到 \[ \frac{\partial S}{\partial a_i} = 0, i \in [0, m] \] 此时进行推广,我们一般不会一直使用多项式(or 幂函数)去做最小二乘法拟合,有时也会使用其他的初等函数比如\(sinx、e^x\)等
因此设\(\psi(x) = a_0\psi_0(x) + a_1\psi_1(x) + a_2\psi_2(x) + ... + a_m\psi_m(x)\)
此时由\(\frac{\partial S}{\partial a_i} = 0\)可得到如下方程组
\[ \sum_{i=0}^{n}\psi_k(x_i)[a_0\psi_0(x_i) + a_1\psi_1(x_i) + a_2\psi_2(x_i) + ... + a_m\psi_m(x_i) - y_i] = 0, k \in [0, m] \]
此处引用如下记号
\[ \begin{cases} (\psi_k, \psi_j) = \sum_{i = 0}^{n}\psi_k(x_i)\psi_j(x_i)\\ (\psi_k, f) = \sum_{i = 0}^{n}\psi_k(x_i)y_i \end{cases} \]
因此可以将上一条列出的线性方程组转化为矩阵乘积
\[ \begin{bmatrix} (\psi_0, \psi_0) & (\psi_0, \psi_1) & ... & (\psi_0, \psi_n)\\ (\psi_1, \psi_0) & (\psi_1, \psi_1) & ... & (\psi_1, \psi_n)\\ : & : & & :\\ (\psi_n, \psi_0) & (\psi_n, \psi_1) & ... & (\psi_n, \psi_n) \end{bmatrix} \begin{bmatrix} a_0\\a_1\\:\\a_n \end{bmatrix} = \begin{bmatrix} (\psi_0, y_0)\\(\psi_1, y_1)\\:\\(\psi_n, y_n) \end{bmatrix} \]