数值微分
为了能够通过有限的离散已知点,推算一个函数在某一点处的导数值,这类问题称为数值微分
用插值构造数值微分公式
为了能够得到任意点的导数值,我们一般先用插值多项式\(p_n(x)\)拟合目标函数\(f(x)\),再根据插值多项式求导来求导数值
插值构造微分的余项

注意:这里得到的插值构造微分的余项公式中,当带入所有已知离散点\(x_0, x_1, ..., x_n\),都能得到等号右边,加法右边的\(w_{n+1}(x)\)为0,因此当我们要求的导数点就是我们已知的离散点\(x_i\)时,余项就是 \[ \begin{equation} f'(x_i) - p_n'(x) = \frac {f^{(n+1)}(\xi)} {(n+1)!}w_{n+1}'(x) \end{equation} \]
常见的插值构造微分公式
三点近似插值公式 \[ \begin{cases} f'(x_0) = {1 \over 2h} [-3f(x_0) + 4f(x_1) - f(x_2)]\\ f'(x_1) = {1 \over 2h} [-f(x_0) + f(x_2)]\\ f'(x_2) = {1 \over 2h} [f(x_0) -4f(x_1) + 3f(x_2)] \end{cases} \] 对于导数估值的余项分析,采用上述得到的余项公式计算即可,因为这里的三点公式所求导数点都是已知点\(x_i\)
数值积分
一切数值积分公式都满足以下特点 \[ \int_{a}^{b}f(x)dx = \sum_{k = 0}^{n}A_kf(x_k) \] 即利用已知离散点得函数值,以及各个公式要求得待定系数得到积分的近似公式
插值构造数值积分
由于所有插值多项式计算公式最终得到的多项式结果仅与离散点有关,因此此处采用lagrange插值公式进行带入 \[ \int_{a}^{b}f(x)dx = \int_{a}^{b} \prod_{j \ne k \atop j = 0}^{n} \frac{x - x_j}{x_k - x_j}f(x_k)dx\\ \Rightarrow A_k = \int_{a}^{b} \prod_{j \ne k \atop j = 0}^{n} \frac{x - x_j}{x_k - x_j}dx \] 以上得到插值构造数值积分中的待定系数恰为lagrange插值公式中每一个离散点的系数
插值构造数值积分的余项 \[ R_n[f] = \int_{a}^{b}f(x)dx - \sum_{k = 0}^{n}A_kf(x_k) = \int_{a}^{b}f(x) - p_n(x)dx = \int_{a}^{b}\frac{f^{(n+1)}(\xi)}{(n+1)!}w_{n+1}(x)dx \] 显然,由多项式插值余项公式的积分可以直接得到当前插值构造数值积分的余项
代数精度
当数值积分公式的一系列系数确定以后,对这个数值积分公式的代数精度做出以下评定:
对于任何次数不超过m,但对于m+1次代数多项式不能准确成立,则称该数值积分公式有m次代数精度
关于代数精度的详细验证,则每个次数阶上仅使用对应的幂函数\(x^p\)进行数值积分验证即可
Newton-Cotes公式
当已知离散点都是等距离点时,可以使用Newton-Cotes公式代系数进行计算,至于使用梯形公式 n=1、simpson公式 n=2还是Cotes公式 n=4取决于你当前已知的离散点数量
梯形公式 \[ \int_{a}^{b}f(x)dx = \frac{(b-a)}{2}[f(a) + f(b)] \\ \]
余项分析,先有以下公式 \[ R_1[f] = \int_{a}^{b}R_n(x)dx = \int_{a}^{b}\frac{f''(\xi)}{2}w_1(x)dx =\int_{a}^{b}\frac{f''(\xi)}{2}(x - a)(x - b)dx \] 使用
积分第二中值定理\[ \int_{a}^{b}\frac{f''(\xi)}{2}(x - a)(x - b)dx = \frac{f''(\eta)}{2}\int_{a}^{b}(x-a)(x-b)dx\\ \Rightarrow O(h^3) \]Simpson公式 \[ \int_{a}^{b}f(x)dx = { { (b - a) \over 6}[f(a) + 4f(\frac{a + b}{2}) + f(b)]}\\ \] 余项分析 \[ R_2[f] = \int_{a}^{b}\frac{f^{(3)}(\xi)}{3!}w_3(x)dx\\ \Rightarrow O(h^5) \]
Cotes公式 \[ \int_{a}^{b}f(x)dx = \frac{(b - a)}{32}[7f(x_0) + 32f(x_1) + 12f(x_2) + 32f(x_3) + 7f(x_4)] \] 余项分析 \[ R_4[f] = \int_{a}^{b}\frac{f^{(5)}(\xi)}{5!}w_5(x)dx\\ \Rightarrow O(h^7) \]
代数精度判定定理1:当有n+1个结点的插值公式计算得到的数值积分公式,其代数精度至少为n
注意定理1适用于所有插值公式得到的数值积分公式,但是注意这里对代数精度的判定只有至少这个程度,并不能准确的判断代数精度,而具体代数精度在具体题目中,可能需要以此讨论幂次递增的幂函数来验证一个公式的代数精度
代数精度判定定理2:设\(f(x)\)在\([a, b]\)有n+2阶导数 \[ R_n[f] = \begin{cases} {f^{(n+2)}(\xi) \over (n+2)!} \int_{a}^{b}xw_{n+1}(x)dx, n为偶数\\ {f^{(n+1)}(\xi) \over (n+1)!} \int_{a}^{b}w_{n+1}(x)dx, n为奇数 \end{cases} 其中\xi \in [a, b]\\ 此处存疑,未能理解公式含义\\ 看起来好像是代数精度的可确定下限可由余项的导数阶减一确定 \] 当n为奇数时,Newton-Cotes公式的代数精度至少为n;当n为偶数时,Newton-Cotes公式的代数精度至少为n+1
复合低阶Newton-Cotes公式
复合求积公式
当我们的需要求解的积分区间过大时,直接套用Newton-Cotes公式最造成误差偏大,此时可以将大区间拆解成一个个小区间,并在小区间上依次套用相同阶的Newton-Cotes公式,最终得到低阶复合Newton-Cotes公式
复合梯形公式 \[ \int_{a}^{b} f(x)dx = \sum_{k = 0}^{n - 1}\int_{x_k}^{x_{k+1}}f(x)dx\\ = \sum_{k = 0}^{n - 1} \frac{h}{2} [f(x_k) + f(x_{k+1})]\\ = \frac{h}{2}[f(a) + 2\sum_{k = 1}^{n - 1}f(x_k) + f(b)] \]
复合Simpson公式
\[ \int_{a}^{b} f(x)dx = \sum_{k = 0}^{n - 1}\int_{x_k}^{x_{k+1}}f(x)dx\\ = \frac{h}{6}\sum_{k = 0}^{n - 1}[f(x_k) + 4f(x_{k + \frac{1}{2}}) + f(x_{k+1})], 注意此处x_{k + \frac{1}{2}}表示x_k和x_{k+1}的中点\\ = \frac{h}{6}[f(a) + 4\sum_{k = 0}^{n - 1}f(x_{k+\frac{1}{2}}) + 2\sum_{k = 1}^{n - 1}f(x_k) + f(b)] \]
复合求积公式的收敛阶
定义:如果一种复合求积公式\(I_n\),有如下特性,则定义该收敛阶 \[
\lim_{h \rightarrow0} \frac{I-I_n}{h^p} = c, c为常数
\] 此时称该求积公式\(I_n\)的收敛阶为p
已知上述两种复合公式的余项分别是\(O(h^2)\)和\(O(h^4)\),而且两个公式的收敛阶也分别是2、4
误差事后估计
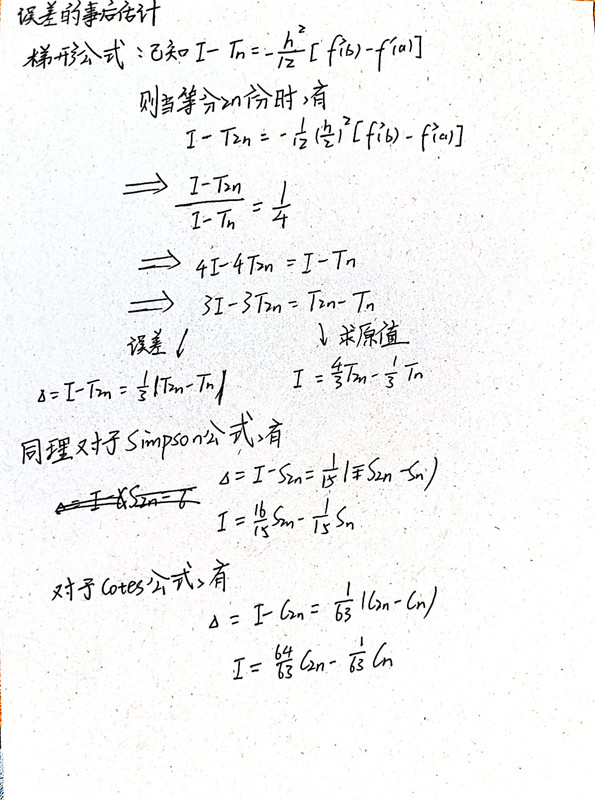
变步长复合梯形求积公式
对于复合梯形求积公式,有如下特点
当我们选择求\(T_n\)时,会将区间分为n份,也就是包括区间的两个端点在内总共有n+1个点用于分隔,那么在有\(T_n\)的基础上求\(T_{2n}\)时,从几何数轴上看就是在已有的分割点之间再加一组分割点。因此衍生出如下变步长求积公式 \[ T_{2^k} = \frac12T_{2^{k-1}} + \frac{b-a}{2^k} \sum_{i=1}^{n}f[a + (2i-1)\frac{b-a}{2^k}] \]
Romberg算法
根据上述提到的误差事后估计算法,做出如下公式总结 \[ \begin{cases} \varDelta = I - I_n = \frac13(T_{2n} - T_n)\\ I = \frac43T_{2n} - \frac13T_n \end{cases} \begin{cases} \varDelta = I - I_n = \frac{1}{15}(S_{2n} - S_n)\\ I = \frac{16}{15}S_{2n} - \frac{1}{15}S_n \end{cases} \begin{cases} \varDelta = I - I_n = \frac{1}{63}(C_{2n} - C_n)\\ I = \frac{64}{63}C_{2n} - \frac{1}{63}C_n \end{cases} \]
利用上述的恶道的3组公式,可以得到Romberg求积迭代的公式,其思想主要是先使用梯形公式组中的\(I\)估计作为下一组的\(S_n\),而由Simpson公式得到的\(I\)同样作为下一组Cotes公式的\(C_n\)进行带入,在这些公式的嵌套过程中可能会使用到\(T_{4n}, T_{8n}, S_{4n}\)等高阶变步长迭代结果,因此可以画出类似计算差商结果计算的递进图,来画出Romberg算法中从\(梯形 \rightarrow Simpson \rightarrow Cotes\)的积分近似